Franks Motorrad-Seite

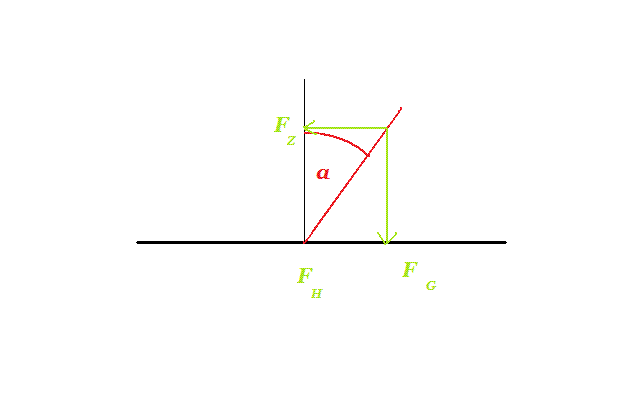
    Schräglage und Haftung

Der Kamm'sche Kreis

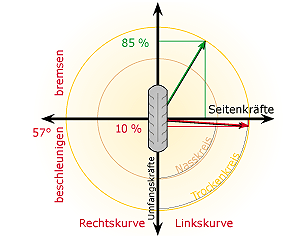
Der Kamm'sche Kreis gehört zu den bekanntesten Darstellungen des Zusammenhanges zwischen den Beschleunigungsreserven, sowohl negativer (=Bremsung), als auch positiver (=Gasgeben) Natur eines Motorrades in Schräglage. Das Problem des Kamm'schen Kreises ist, daß er es nicht ermöglicht, die Beschleunigungsreserven in Abhängigkeit der Motorrad-Schräglage abzulesen. Denn der dargestellte Winkel zwischen Schräglagenhaftung ("Seitenkäfte") und Beschleunigungsreserve entspricht nicht dem Schräglagenwinkel.

Deshalb wird nachfolgend eine realistischere Darstellung der Beziehung vorgestellt.

Beziehung zwischen Schräglagenwinkel und Beschleunigungsvermögen

  M := Massenschwerpunkt des Motorrades + Fahrer
  m := Masse des Motorrades + Fahrer
  g := Graviationskonstante (= Erdbeschleunigung)
  a := Beschleunigung des Motorrades
  μ := Reibbeiwert  (Bsp trockenerAsphalt: μ = 1)

  α : = effektiver (physikalischer) Schräglagenwinkel des Motorrades
  F_G := Gesamtgewicht des Motorrades + Fahrer
  F_z := Zentripedalkraft ("Fliehkraft")
  F_a := Beschleunigungskraft des Motorrades 
  F_μ := maximale Haftreibung

Es gilt: Beschleunigungskraft F_a im Massenzentrum: (I.a) F_a = m a
Haftkraft: ("Fliehkraft") (I.b) F_μ = μ F_G = μ m g
Befindet sich das Motorrad in "stabiler Schräglage", so heben sich Zentripedalkraft und das "Umfallmoment", das durch das "überhägende" Gewichts des Motorrades entsteht, gegenseitig auf. Man sieht leicht: F_z (II.a) —————— = tanα F_G
oder: (II.b) F_z = F_G tanα = m g tanα
Maximal mögliche Beschleunigung und Zentripedalkraft ergänzen sich vektoriell zur maximalen Haftkraft, so daß mit Phytagoras gilt: (III.a) F_μ² = F_G² + F_z²
(III.a beschreibt den Kamm'schen Kreis. Wie man sieht, ist der "Winkel" des Kamm'schen Kreises rein trigonometrischer Natur)

Mit I.a, I.b und II.a wird aus III.a:

  (III.b)    g² μ² = a² + g² tan²α

ergo folgt für die Beschleunigungsreserve in Einheiten von g (ca 10m/s²): (III.c) a/g = (μ² - tan²α)^1/2
Aus dem nachfolgenden Plot für verschiedene Reibbeiwerte μ kann man einige interessante Aspekte entnehmen:

mögl. Beschleunigung a in g (=10 m/s²) μ a(α , μ=1,5) a(α , μ=1,0) a(α , μ=0,5) eff. Schräglagenwinkel α

Betrachtet sei zunächst Reibbeiwert μ=1:

bei "null" Grad Schräglage beträgt die maximale Beschleunigung 1 g.
die maximale (physikalische) Schräglage ist bei 45^o erreicht (hier ist die maximale Haftung aufgebraucht). Auf Grund der Reifenbreiten wird die geometrische Schräglage etliche Grad darüber liegen. D.h. mit Sportreifen bei normalen Straßenverhätnissen können Schräglagen von ca 50 Grad erreicht werden.
bis 30 Grad Schräglage können ständig mehr als 80% der maximalen Beschleunigung umgesetzt werden. Dies ist besonders interessant im Hinblick auf das Thema "Bremsen in Schräglage": d.h. bei im Straßenverkehr üblichen Schräglagen kann fast genau so stark gebremst werden wie mit aufrechtem Motorrad. Allerdings kann hier ein überbremstes Rad schwieriger abgefangen werden als bei aufrechtem Motorrad
bei 40 Grad Schräglage beträgt die Beschleunigungsreserve immer noch 50%

Im Falle von Reibbeiwert μ=1,5 (Slicks auf Rennstrecke) sieht man, daß geometrische Schräglagen von über 60 Grad erreichbar sind.